Description

Une démarche classique pour trouver plus facilement les vertex secondaires est de limiter la recherche en sélectionnant les traces qui passent loin du vertex primaire en établissant une coupure sur le paramètre d'impact. En réalité, l'idéal serait de reconstruire le vertex primaire avec les traces de faible paramètre d'impact (à moins de 5 $\sigma$, paragraphe ) puis de reconstruire le vertex secondaire uniquement avec les traces incompatibles avec le vertex primaire. Dans notre cas, parmi toutes les traces reconstruites, seules les traces dont le paramètre d'impact dans le plan transverse (au faisceau) est supérieur à $3 \sigma$ seront conservées (où $\sigma$ est l'erreur sur la position par rapport à l'axe du point d'impact). Ce choix de coupure est justifié au paragraphe . Ces traces sélectionnées permettent de déterminer la position de l'ensemble des vertex candidats comme l'intersection de 2 traces sélectionnées. Chacun de ces vertex candidats est nécessaire comme point de départ à l'algorithme EA et est appelé "vertex seed". 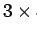On conservera uniquement les "vertex seed" si leur $\chi^2$ est inférieur à 20, sachant que le 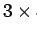$\chi^2$ est d'autant plus faible que la reconstruction est précise.

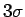Ensuite, pour chaque itération en température $T$ et pour chaque couple (trace i, "vertex seed" j), l'agorithme itératif EA détermine le potentiel d'attraction $V_{i,j}$ (une distribution de Boltzman en 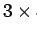$\chi^2$) défini par

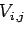$$V_{i,j} = \frac{e^{-\chi^2_{i,j} / T}}{e^{-\Lambda / T} + \Sigma_j e^{-\chi^2_{i,j} / T}}$$ (3)

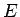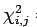• où $\chi^2_{i,j} = P\text{ }E^{-1} \text{ }^TP$, avec $E$ la matrice d'erreur en position de la trace $i$ et le vecteur $P$ la distance entre la trace $i$ et le "vertex seed" $j$ ($\text{ }^tP$ est le transposé du vecteur $P$);
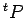• où $\Lambda = 4$ et permet le calcul du potentiel 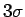$V_{i,j}$ en tenant compte des traces isolées;
• et où $T$ est sans unité et 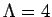$T = 200/k$ avec $k$ l'indice itératif variant entre 1 et 50 par pas de 1. On remarque que la température $T$ baisse fortement au départ (elle passe de 200 à 50 en 4 itérations) éliminant ainsi rapidement les "vertex seed" mal placés puis elle baisse plus progressivement pour laisser aux autres vertex trouver "naturellement" leur position.

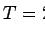En observant l'équation , on peut vérifier que plus les traces sont éloignées, plus le $\chi^2_{i,j}$ est important et moins le potentiel d'attraction 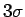$V_{i,j}$ est important. Mais ce potentiel varie assez peu en fonction de l'itération en température $T$.

L'objectif de ce potentiel d'attraction 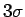$V_{i,j}$ est de déterminer la valeur du déplacement de chaque "vertex seed". En effet, pour chaque température $T$ et pour chaque trace $i$, les "vertex seed" $j$ se déplacent de (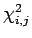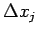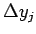$\Delta x_j$, $\Delta y_j$, $\Delta z_j$) définis par :

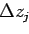$$(\Delta x_j, \Delta y_j, \Delta z_j) = -\eta \times \Sigma_j... ... \partial d_{i,j}/\partial y_j, \partial d_{i,j}/\partial z_j)$$ (4)

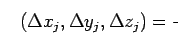• où $\eta = 0,5 \times 10^{-4}/k^{0,8}$ détermine l'ordre de grandeur du déplacement;
• et où les dérivées 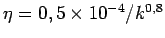$(\partial d_{i,j}/\partial x_j, \partial d_{i,j}/\partial y_j, \partial d_{i,j}... ...l x_j, \partial \chi^2_{i,j}/\partial y_j, \partial \chi^2_{i,j}/\partial z_j)$ sont calculées numériquement par pas de 1 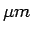$\mu m$ sur les axes $x$, $y$ et $z$.

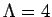Toutes les traces $i$ contribuent donc à déterminer la position de ces "vertex seed" $j$. De plus, on remarque que plus l'itération $k$ augmente, plus la température $T$ diminue ($T = 200/k$) et moins les "vertex seed" peuvent se déplacer. On dit que le système des "vertex seed" se refroidit peu à peu. La fonction de minimisation d'énergie est alors $E=\frac{1}{\beta} \Sigma_i log(e^{-\beta \Lambda + \sigma_j e{-\beta \chi^2_{i,j}}})$.

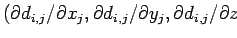L'algorithme EA possède aussi une fonction de fusion des vertex très proches : si 2 "vertex seed" sont distants de moins de 100 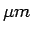$\mu m$, on ne garde qu'un seul "vertex seed". Ce processus de fusion est effectué à la fin de chaque itération en température.

L'algorithme EA arrête les itérations en température pour trois types de cas :

• Cas 1: tous les "vertex seed" convergent en position (déplacement entre 2 itérations en température inférieur à 20 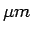$\mu m$) après au moins 3 itérations en température,
• Cas 2: tous les "vertex seed" divergent en position (déplacement entre 2 itérations en température supérieur à 500 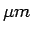$\mu m$) après au moins 3 itérations en température,
• dans tous les autres cas : arrêt à la 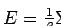$50^{eme}$ itération.

A la fin des itérations en température, chaque trace est associée au "vertex seed" le plus proche. Notons que les "vertex seed" associés à moins de 2 traces sont éliminés. Puis lorsque l'on a identifié toutes les traces provenant d'un même vertex, on utilise la méthode de linéarisation (la classe LinearVertexFitter). Cette méthode itérative est basée sur l'approximation des traces par des droites (au voisinage du vertex), et le point où la trace est tangente à cette droite est appelé point de linéarisation. La position du vertex est déterminé par l'intersection de ces droites (figure ). 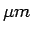Cette méthode très rapide fournit une estimation très précise de la position du vertex, avec une erreur de moins de 1 $\mu m$ (si la distance entre le point de linéarisation et le vertex est de moins de 1 mm) [KAR97].

Figure: Illustration de la méthode de linéarisation : les trajectoires sont approximées par des droites dont l'intersection fournit la position du vertex.

Cette méthode nous permet d'obtenir la position finale et le nombre final des vertex reconstruits par l'algorithme EA.