Reconstruction de vertex primaires et l'empilement d'événements

Une étude de reconstruction de vertex primaire par la méthode de "binning" (partie ) a été faite pour 150 événements $q$ $\bar{q}$ avec empilement d'événements. Dans notre cas, on définit l'événement "intéressant" comme l'événement qui a été sélectionné par le système de déclenchement et qui entraîne l'acquisition. Cet empilement d'événements sur l'événement "intéressant" (partie ) apporte 15 fois plus de traces, mais la plupart de ces traces sont de faible impulsion. On peut alors distinguer facilement le vertex primaire associé à l'événement "intéressant" en choisissant le vertex primaire reconstruit ayant à la fois la plus grande impulsion transverse $^($¹⁹$^)$ et le plus grand nombre de traces associées (figures et ).

Figure: Le nombre de traces associées à un vertex primaire en fonction de la somme des impulsions transverses des traces associées à ce vertex.

Figure: Le nombre de traces associées à un vertex primaire en fonction de la somme des impulsions transverses des traces associées à ce vertex.

On se rend compte que ces deux conditions sont nécessaires car on reconstruit parfois des vertex primaires associés à un grand nombre de traces mais avec une impulsion transverse de quelques GeV au lieu des quelques dizaines de GeV attendus mais parfois le choix est plus complexe. Sur la figure , on observe deux vertex associés à un grand nombre de traces :

• un vertex associé à 30 traces et avec une impulsion transverse de 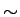$\sim$ 49,1 GeV, ce qui équivaut à 1,6 GeV/trace;
• un vertex associé à 12 traces et avec une impulsion transverse de 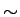$\sim$ 59,5 GeV, ce qui équivaut à 5 GeV/trace.

Le vertex primaire de l'événement "intéressant" est le deuxième vertex car il est associé à des traces plus énergétiques.

Le fait de bien reconstruire la coordonnée $z$ des vertex primaires est relativement simple. Mais reconstruire les trois coordonnées des vertex secondaires (associés à un nombre plus faible de traces) demande un algorithme de reconstruction plus complexe.